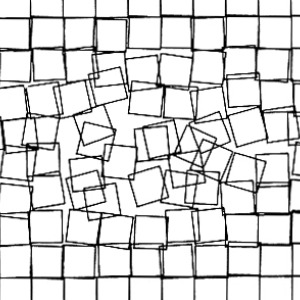
La grille, se déplacer sur deux dimensions
| Artiste | Œuvre | Année |
|---|---|---|
| William Kolomyjec | Boxes I | 1977 |
Segmenter l'espace à l'aide de la boucle for
background(255);
noFill()
strokeWeight(3)
stroke(50)
const CELL_SIZE = 80
const COLROW = width / CELL_SIZE
const HALF_COLROW = (COLROW / 2)
push()
translate(0.025 * width, 0.025 * height)
scale(0.95)
for (let x = 0; x < COLROW; x++) {
for (let y = 0; y < COLROW; y++) {
const e = 1 - sin(
sqrt(
(x - HALF_COLROW) ** 2 +
(y - HALF_COLROW) ** 2
) / COLROW * 3)
const _e = max(e, 0.001)
const rot = random(-_e, _e) * HALF_PI
push()
translate(
x * CELL_SIZE + random(-CELL_SIZE, CELL_SIZE) * _e,
y * CELL_SIZE + random(-CELL_SIZE, CELL_SIZE) * _e
)
push()
rotate(rot)
rect(0, 0, CELL_SIZE * 0.9, CELL_SIZE * 0.9)
pop()
pop()
}
}
pop()
La grille
Dans cette première leçon, nous verrons comment créer une grille à l'aide de la boucle for() et comment se repérer horizontalement et verticalement en fonction de la taille des cellules CELL_SIZE.
Ici, on commence par définir la taille des cellules puis on calcul le nombre de cellules dans une rangée ou dans une colonne.
const CELL_SIZE = 60
const COLROW = width / CELL_SIZESi l'on veut faire l'inverse, définir le nombre de cellules et calculer à partir de cette valeur la taille des cellules, on inversera les deux déclarations.
const COLROW = 30
const CELL_SIZE = width / COLROWEnsuite, on va commencer parcourir les colonnes avec une première boucles for().
for (let x = 1; x < COLROW-1; x++) {L'instruction se décompose en trois étapes (séparée par des points virgules), on initialise la variable x puis on lui donne comme limite le nombre de colonnes et, ensuite, on indique qu'à chaque boucle, on va additionner 1 à la valeur de x. À chaque fois que la valeur de x change, à chaque fois qu'elle s'incrémente, le code contenu entre les accolades sera exécuter.
À ce stade, on ne peut tracer que la première cellule de chaque colonne, on se déplace pour l'instant que sur l'axe horizontal, pour que l'on puisse se déplacer sur l'axe vertical, on va utiliser une deuxième boucle for().
for (let x = 1; x < COLROW-1; x++) {
// On se déplace d'une cellule vers la droite jusqu'à atteindre le nombre total de colonnes
for (let y = 1; y < COLROW-1; y++) {
// On se déplace d'une cellule vers le bas jusqu'à atteindre le nombre total de rangées
}
}En inversant les deux boucles, on change l'ordre de construction, ci-dessus, on construit les cellules dans les colonnes alors que, ci-dessous, on construit les cellules dans les rangées.
for (let y = 1; y < COLROW-1; y++) {
// On se déplace d'une cellule vers le bas jusqu'à atteindre le nombre total de rangées
for (let x = 1; x < COLROW-1; x++) {
// On se déplace d'une cellule vers la droite jusqu'à atteindre le nombre total de colonnes
}
}Créer des variations entre les cellules de la grille
La variable e est plus complexe, si elle vous effraie, ne vous attarder pas dessus, retenez qu'elle permet de savoir, sur une échelle de 0 à 1, si la cellule est proche du centre de la composition (0=loin, 1=le centre).
const e = 1 - sin(
sqrt(
(x - HALF_COLROW) ** 2 +
(y - HALF_COLROW) ** 2
) / COLROW * 3
)Elle utilise le triangle rectangle de Pythagore pour évaluer la distance, x - HALF_COLROW permet de soustraire le centre horizontal à la valeur de x. Quand x vaut 1 puis 2, 3, 4, 5, 6, cela donne -2, -1, 0, 1, 2 et 3. Ainsi, la distance de la cellule sera négative si elle est à gauche du centre ou positive si elle est à doite.
La plupart des autres instructions permettent de calculer l'hypoténuse :
- on éleve les distances horizontales et verticales au carré
** 2 - on additionne les valeurs des deux dimensions (x et y)
- on obtient l'hypoténuse avec
sqrt()(racine carrée) qui correspond à la distance entre notre cellule et le centre de la composition.
Ensuite, on divise cette valeur par une échelle de grandeurs COLROW * 3 et on lui applique un sinus sin() pour qu'elle soit comprise entre 0 et 1.
Finalement, on inverse cette valeur pour qu'elle soit plus grande au centre qu'au bord, en la soustrayant à 1.
Il ne nous reste plus qu'à appliquer cette valeur pour faire pivoter nos cellules.
const rot = random(-_e, _e) * HALF_PIOu pour les déplacer
translate(
x * CELL_SIZE + random(-CELL_SIZE, CELL_SIZE) * _e,
y * CELL_SIZE + random(-CELL_SIZE, CELL_SIZE) * _e
)Dans ces deux instructions, on appelle la fonction random() qui permet de créer un chiffre aléatoire.
Quand cette fonction est appelée avec deux arguments random({1}, {2}), l'aléatoire est calculé en fonction d'un minimum {1}, et d'un maximum {2}.
Ici, on utilise notre variable de distance ce qui nous permet d'appliquer des rotations et des déplacements plus grands au centre qu'aux bords de la composition.
Ce qu'il faut retenir
| USAGE | TYPE | |
|---|---|---|
for() |
permt de répéter des instruction un certain nombre de fois, en ayant un compteur qui nous indique la progression | BOUCLE |
random() |
permet de créer un nombre aléatoire | FONCTION |